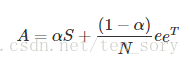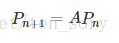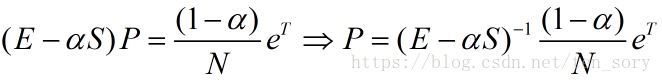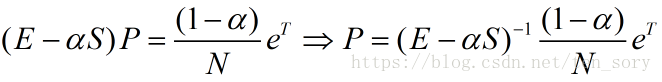目标一 迭代法实现
题目
迭代法实现大规模PageRank,网页数量不低于10000
思路
首先创建一个txt文件,里面储存各个点之间的关系,然后通过python语言读取,将其转化为矩阵,并通过公式将其转化为相应矩阵,然后进行迭代,直至误差小于 0.00000001结束。
原理
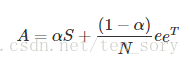
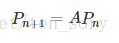
源代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
| import numpy as np
if __name__ == '__main__':
file = open('input2.txt', 'r')
edges_in = []
edges_out = []
while True:
lines = file.readline().strip('\n')
if not lines:
break
else:
this_line = lines.split(' ')
edges_out.append(this_line[0])
edges_in.append(this_line[1])
nodes = []
for edge in edges_out:
if edge not in nodes:
nodes.append(edge)
for edge in edges_in:
if edge not in nodes:
nodes.append(edge)
length = len(nodes)
i = 0
node_to_num = {}
for node in nodes:
node_to_num[node] = i
i += 1
for i in range(len(edges_in)):
edges_in[i] = node_to_num[edges_in[i]]
edges_out[i] = node_to_num[edges_out[i]]
S = np.zeros([length, length])
for i in range(len(edges_in)):
S[edges_in[i], edges_out[i]] = 1
for j in range(length):
sum_of_col = sum(S[:, j])
for i in range(length):
if sum_of_col != 0:
S[i, j] /= sum_of_col
else:
S[i, j] = 1/length
a = 0.85
A = a * S + (1 - a) / length * np.ones([length, length])
PageRank1 = np.ones(length) / length
PageRank2 = np.zeros(length)
judge = 1
while judge > 0.00000001:
PageRank2 = np.dot(A, PageRank1)
judge = PageRank2 - PageRank1
judge = max(map(abs, judge))
PageRank1 = PageRank2
print('最终结果:', PageRank1)
|
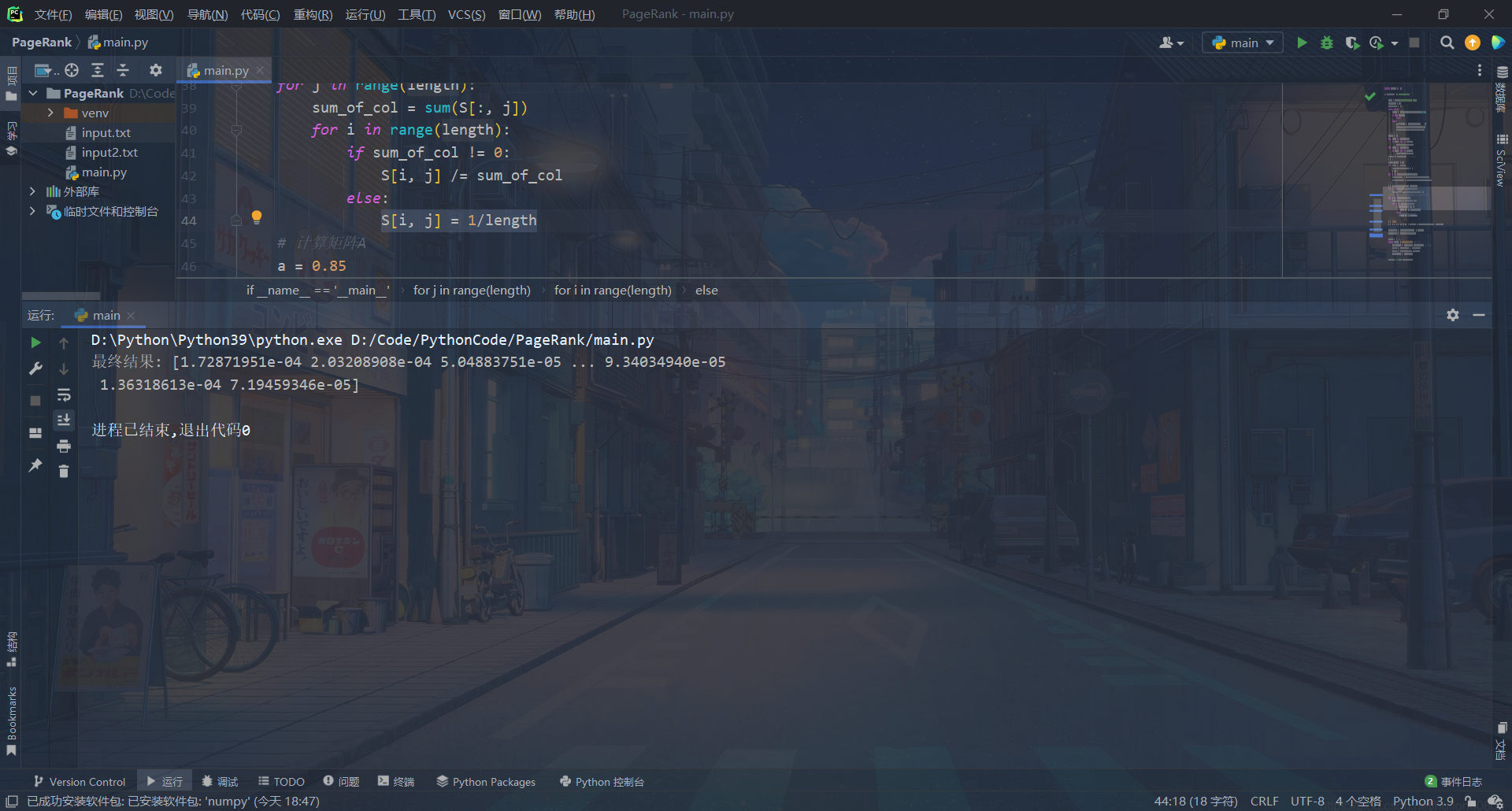
运行截图
注:因为10000个数据不太好展示,所以附带运行了一下10以内的数据进行简单展示。
10以内的简单展示
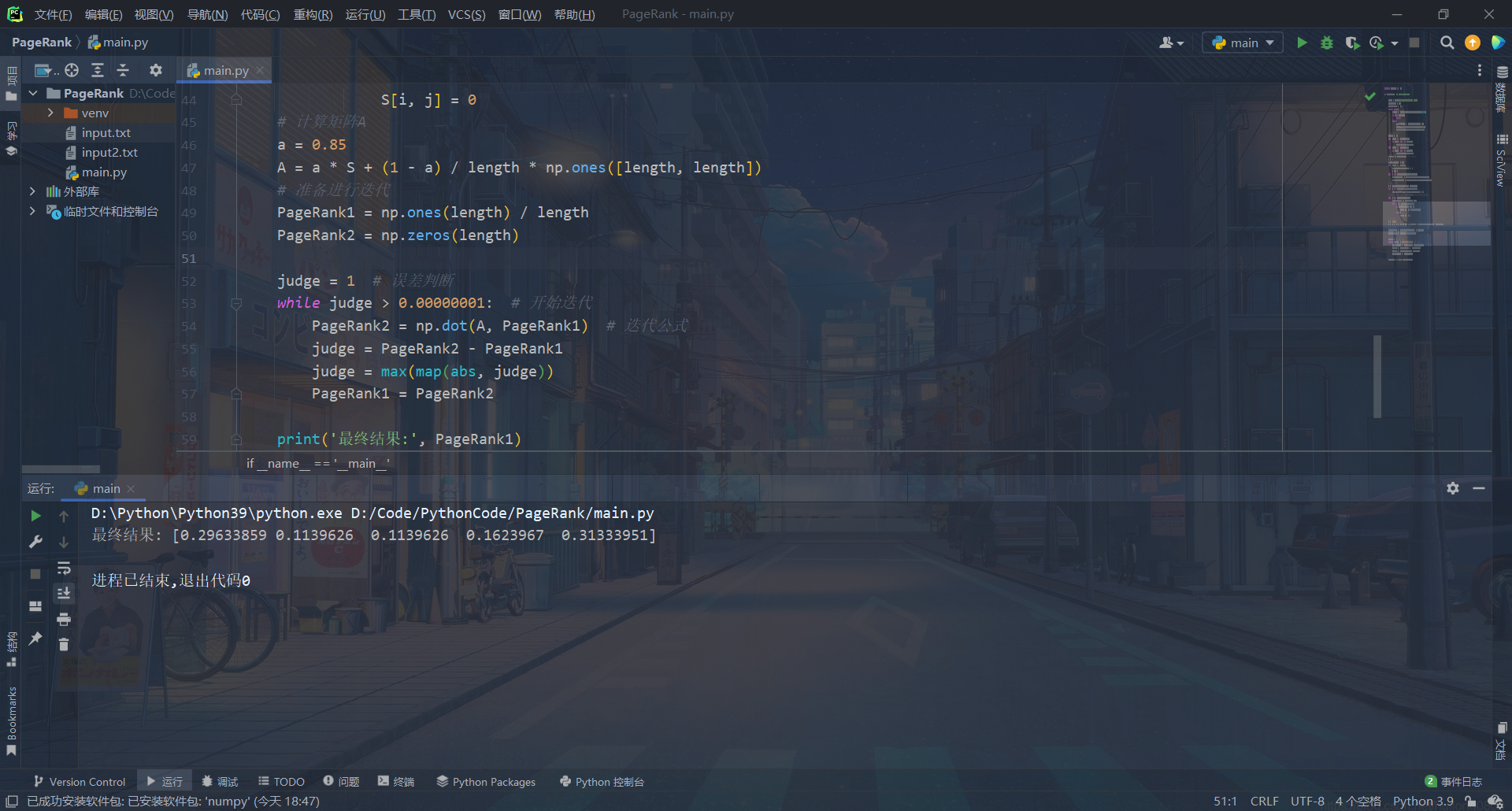

目标二 代数法实现
题目
代数法求小规模PageRank的稳态解,网页数量为5
思路
利用上一个迭代法部分代码求得S与A,然后进行求逆等相应操作。
原理
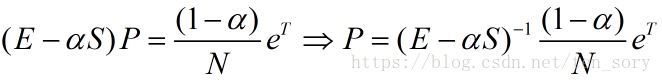
源代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
| import numpy as np
if __name__ == '__main__':
file = open('input.txt', 'r')
edges_in = []
edges_out = []
while True:
lines = file.readline().strip('\n')
if not lines:
break
else:
this_line = lines.split(' ')
edges_out.append(this_line[0])
edges_in.append(this_line[1])
nodes = []
for edge in edges_out:
if edge not in nodes:
nodes.append(edge)
for edge in edges_in:
if edge not in nodes:
nodes.append(edge)
length = len(nodes)
i = 0
node_to_num = {}
for node in nodes:
node_to_num[node] = i
i += 1
for i in range(len(edges_in)):
edges_in[i] = node_to_num[edges_in[i]]
edges_out[i] = node_to_num[edges_out[i]]
S = np.zeros([length, length])
for i in range(len(edges_in)):
S[edges_in[i], edges_out[i]] = 1
for j in range(length):
sum_of_col = sum(S[:, j])
for i in range(length):
if sum_of_col != 0:
S[i, j] /= sum_of_col
else:
S[i, j] = 1 / length
a = 0.85
A = a * S + (1 - a) / length * np.ones([length, length])
E = np.identity(length)
B = np.ones(length)
PageRank = (1 - a) / length * np.linalg.inv(E - a * S)
PageRank = np.dot(PageRank, np.transpose(B))
print('最终结果:', PageRank)
|
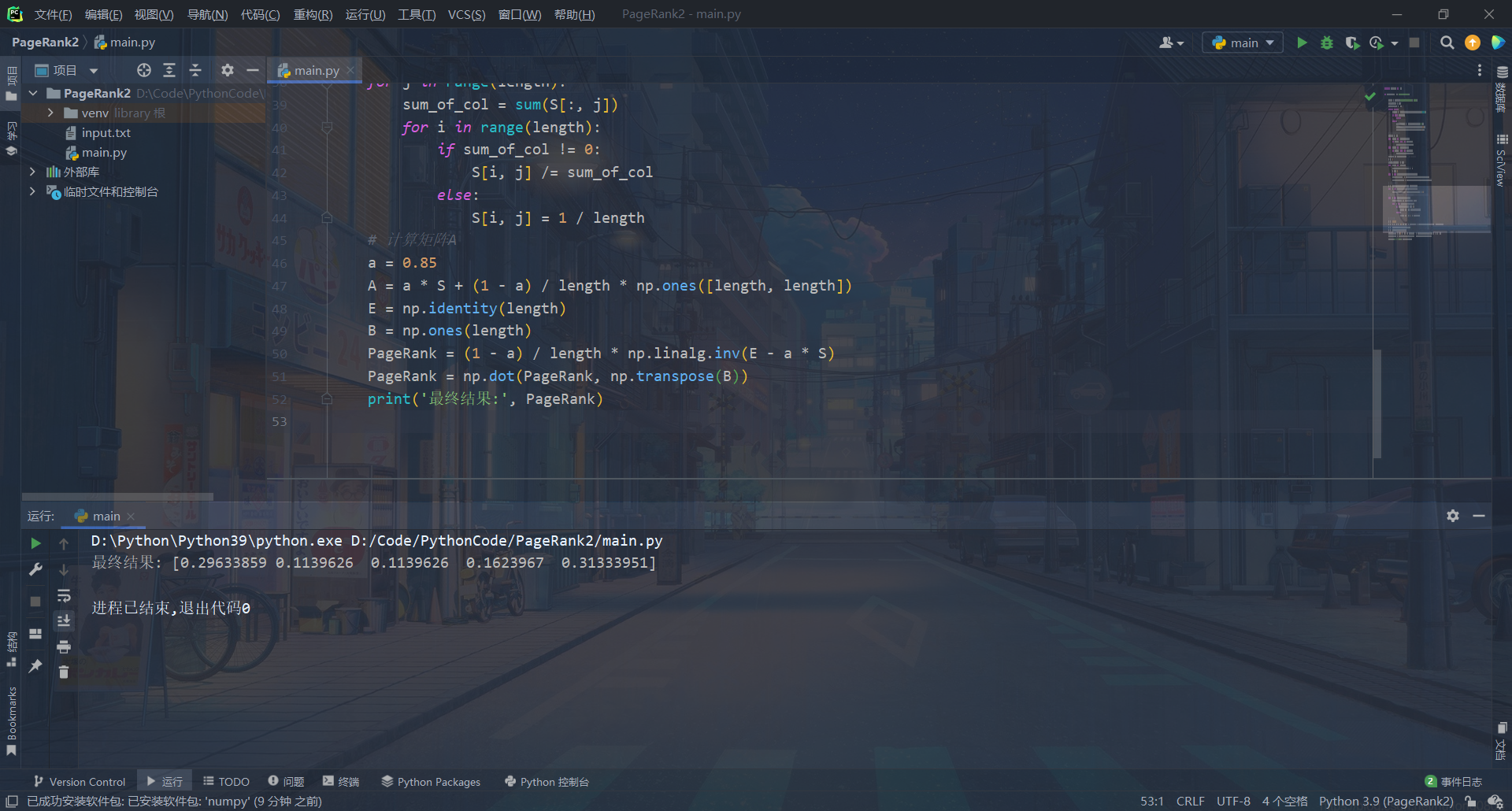
运行截图

附加
题目
构造不存在稳态的情况,设计方法变为有稳态的情况
思路
pagerank的计算公式按迭代方式计算,保证矩阵A是正确的。
A=dP+(1-d)e*e^T/n
0<d<1
源代码
注:本人上述代码均使用了该方法避免不收敛
运行截图
打回后修改
一、打回信息
分数:85
批语:
代数求解方法需要解方程组;变成稳态方法未描述;正常返需要证明
二、修改
1.代数求解方法需要解方程组
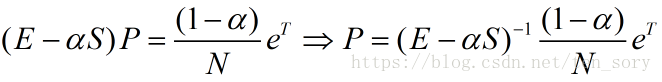
矩阵:S
矩阵:(E-aS)-1
方程:
解之得:
2.变成稳态的方法
利用衰减系数进行判断,用户会有概率随机跳转到一个网页,这样可以保证存在稳态